题目内容
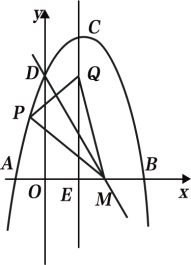
【题目】如图1,抛物线![]()
![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求该抛物线的函数表达式;
(2)动点![]() 在线段
在线段![]() 下方的抛物线上.
下方的抛物线上.
①连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
②过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() 中的一个角恰好等于
中的一个角恰好等于![]() 的2倍?如果存在,求出点
的2倍?如果存在,求出点![]() 的横坐标;如果不存在,请说明理由.
的横坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,1或
;②存在,1或![]()
【解析】
(1)根据题意可求点A(-1,0),点B(m,0),根据OB=3OA,可求m的值,即可求解析式;
(2)①先求出直线BC解析式,即可得F点坐标,利用![]() 可得用含t的代数式表示d;
可得用含t的代数式表示d;
②分∠CDH=2∠ABC或∠DCH=2∠ABC两种情况讨论,利用锐角三角函数,相似三角形的性质可求点D的横坐标.
解:(1)令y=0,则![]() ,
,
∴![]() ,
,
∴(x-m)(x+1)=0
∴![]()
∵m>0,点A在点B的左侧
∴点A(-1,0),点B(m,0)
∴OA=1,OB=m ,
∵OB=3OA ,∴m=3
∴抛物线![]()
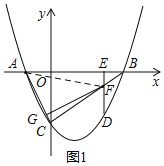
(2)①如图1:连接AF
∵抛物线![]() 与y轴交与点C
与y轴交与点C
∴点C(0,-2)
∵点A(-1,0),点B(3,0),点C(0,-2)
∴AB=4,OC=2,AC=![]()
∵设直线BC解析式y=kx+b
∴![]()
解得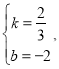
∴直线BC解析式![]()
∵D点横坐标为t,DF⊥AB
∴点F的横坐标为t ∴![]()
∵![]()
∴![]() ,
,
∴ ![]()
∴![]() ,
,
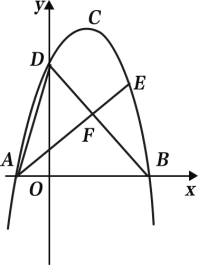
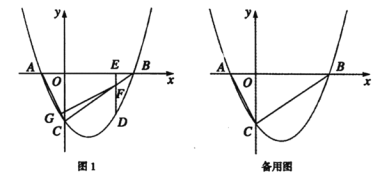
②若∠DCH=2∠ABC,如图2:
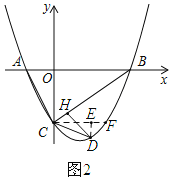
过点C作CF∥AB,交抛物线于F点,作DE⊥CF于点E.
∵AB∥CF ∴∠ABC=∠BCF
又∵∠DCH=2∠BCF
∴∠DCF=∠ABC=∠BCF
∵点D坐标为![]() ,
,
∴CE=t,DE=![]()
∵tan∠DCF=tan∠ABC= ![]()
∴ 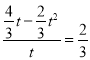
∴![]() (不合题意舍去),
(不合题意舍去),![]()
即点D的横坐标为1.
若∠CDH=2∠ABC,如图3:
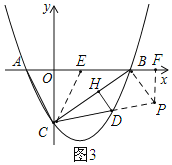
作∠ECB=∠ABC,过点B作BP∥HD,交CD的延长线于点P,作PF⊥AB于F.
∵∠ECB=∠ABC ∴EC=BE,∠AEC=2∠ABC ,
在Rt△OEC中,![]()
∴![]()
![]()
∴CE=![]() ,
,
∴OE=OB-BE=![]() ,
,
∴tan∠AEC=tan2∠ABC=![]()
∵点B(3,0),点C(0,-2)
∴BC=![]()
∵BP∥HD,HD⊥BC ∴BP⊥BC,∠CDH=∠CPB=2∠ABC
∴tan∠CPB=tan2∠ABC=![]() =
=![]() .
.
∴BP=![]()
∵∠ABC+∠PBF=90°,∠ABC+∠OCB=90° ,
∴∠OCB=∠PBF,且∠BOC=∠PFB=90°
∴△BOC∽△PFB ∴ 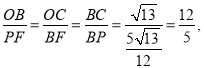
∴PF=![]() BF=
BF=![]()
∴![]()
∴点P坐标![]()
∵点C(0,-2),点P![]()
∴直线PC解析式![]()
∵直线CP与抛物线交于C,D两点
∴ 
解得:![]()
∴点D的横坐标为![]()
综上所述:点D的横坐标为![]() 或1
或1

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?