题目内容
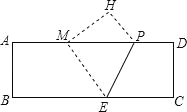
【题目】如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．
（1）求MP的值；
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）
【答案】（1）5；（2）
；（3）7+5
．
【解析】
试题分析：（1）由折叠的性质可得PD=PH=3，CD=MH=4，∠H=∠D=90°，利用勾股定理可得答案；（2）先找到使三角形MEF的周长最小的F点，如图1，做点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，由（1）可得AM，利用勾股定理可得ME和NM′，由△AFM′∽△NEM′，利用相似三角形的性质可得AF；（3）由题意可知，ME,QG的长度是个定值，当四边形MEQG的周长最小时，QE与GM的长度和最小，如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，由平行四边形的判定定理可得四边形ERGQ为平行四边形，由平行四边形的性质可得QE=GR，由垂直平分线的性质易得GM=GM′，可得此时MG+EQ最小，于是四边形MEQG的周长最小，在Rt△M′RN中，易得NR，M′R，从而得到四边形MEQG的最小周长值．
试题解析：（1）∵四边形ABCD为矩形，∴CD=AB=4，∠D=90°，∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，∴PD=PH=3，CD=MH=4，∠H=∠D=90°，∴
=5；（2）如图1，
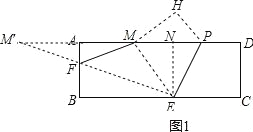做点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，∵AM=AD﹣MP﹣PD=12﹣5﹣3=4，∴AM=AM′=4，∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，∴∠CEP=∠MEP，∠CEP=∠MPE，∴∠MEP=∠MPE，∴ME=MP=5；在Rt△ENM中，MN=
=
=3，∴NM′=11，∵AF∥NE，∴△AFM′∽△NEM′，∴
=
，即
，解得：AF=
，即AF=时，△MEF的周长最小；（3）如图2，
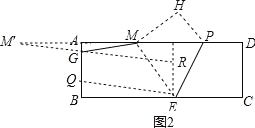由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，∵ER=GQ，ER∥GQ，∴四边形ERGQ是平行四边形，∴QE=GR，∵GM=GM′，∴MG+QE=GM′+GR=M′R，此时MG+EQ最小，四边形MEQG的周长最小，在Rt△M′RN中，NR=4﹣2=2，M′R=
=5
，∵ME=5，GQ=2，∴四边形MEQG的最小周长值=5+2+5=7+5
．
