��Ŀ����
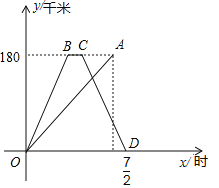
����Ŀ���졢�����ֱ�����180ǧ�ļס�������ͬʱ��������ͬһ·��������ʻ��������У��쳵�����ҵ�ͣ��һ��ʱ���ԭ·ԭ�ٷ��ؼأ���������رȿ쳵�������![]() Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룮�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ���ڿ쳵���ҵط��ؼصĹ����У�������ǡ���ڿ쳵ǰ������쳵���80ǧ��·��ʱ��������ʻ���ܵ�ʱ����_____Сʱ��
Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룮�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ���ڿ쳵���ҵط��ؼصĹ����У�������ǡ���ڿ쳵ǰ������쳵���80ǧ��·��ʱ��������ʻ���ܵ�ʱ����_____Сʱ��
���𰸡�![]()
��������
��������������졢���������ٶȣ�������쳵���ع�����y��ǧ�ף���x��Сʱ���ĺ�����ϵʽ������������г���Ӧ���̼�����⣮
�⣺�������ٶȣ�180����![]() ����60ǧ��/ʱ��
����60ǧ��/ʱ��
�쳵���ٶȣ�60��2��120ǧ��/ʱ��
�쳵ͣ����ʱ�䣺![]() ��Сʱ����
��Сʱ����
![]() ��Сʱ������C��2��180����
��Сʱ������C��2��180����
��CD�Ľ���ʽΪ��y��kx+b����
��C��2��180����D��![]() ��0�����룬��
��0�����룬��
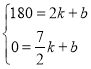 �����
�����![]() ��
��
��쳵���ع�����y��ǧ�ף���x��Сʱ���ĺ�����ϵʽΪy����120x+420��2��x��![]() ����
����
�쳵�Ӽص��ҵ���Ҫ180��120��![]() Сʱ��
Сʱ��
�쳵����֮��60x��80+120��![]() ��
��
���x��![]() ��
��
���ڿ쳵���ҵط��ؼصĹ����У�������ǡ���ڿ쳵ǰ������쳵���80ǧ��·��ʱ��������ʻ���ܵ�ʱ����![]() Сʱ��
Сʱ��
�ʴ�Ϊ��![]()

����Ŀ��Ϊ�˴����л����㴫ͳ�Ļ����н����־�����չ�������ж���У�����ijУ��ί��֯���꼶100��ѧ�������������ж���ѡ�����������ȫ�����ѧ���ijɼ������������õ����в�������ͳ��ͼ����
��� | ������ | Ƶ�� | Ƶ�� |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
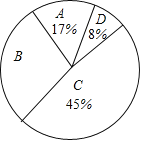
�����������Ϣ������������⣺
(1)����a=___��b=___��
(2)���������ͳ��ͼ��B���Ӧ���ε�Բ�ĽǵĶ�����
(3)��֪������ͬѧ��ȡ��98�ֵ���óɼ������а�������ͬһ�༶�ļס�������ͬѧ��ѧУ����������ͬѧ�����ѡ�������μ��м������������б�������״ͼ����ס�������ͬѧ����ѡ�еĸ��ʡ�