Question

【题目】综合与实践

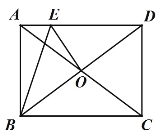
在数学活动课上，老师给出，，．点为的中点，点在射线上运动，将线段绕点逆时针旋转90°得到线段，连接，．过点作，交直线于点．

(1)若点在线段上，如图1，

①根据题意补全图1(不要求尺规作图)；

②判断与的数量关系并加以证明；

(2)若点为线段的延长线上一点，如图2，且，，补全图2，求的面积．

Answer 1

【答案】（1）①见解析；②CF=FH，证明见解析；（2）

【解析】

(1)①依题意补全图1；
②延长DF交AB于点G，根据三角形中位线的判定得出点G为AB的中点，根据中位线的性质及已知条件AC=BC，得出DC=DG，从而EC=FG，易证∠1=∠2=90°-∠DFC，∠CEF=∠FGH=135°，由ASA证出△CEF≌△FGH，所以CF=FH；
(2)依题意补全图3；通过证明△CEF≌△FGH(ASA)得出FC=FH，再求出FC的长，即可解答．

(1)①补全图如图1所示，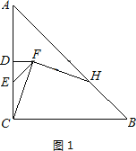

②FH与FC的数量关系是：FH=FC．
证明如下：

如图2，延长DF交AB于点G，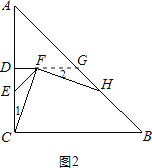

由题意，知∠EDF=∠ACB=90°，DE=DF，
∴DG∥CB，
∵点D为AC的中点，
∴点G为AB的中点，且DC=AC，
∴DG为△ABC的中位线，
∴DG=BC．
∵AC=BC，
∴DC=DG，
∴DC-DE=DG-DF，
即EC=FG．
∵∠EDF=90°，FH⊥FC，
∴∠1+∠CFD=90°，∠2+∠CFD=90°，
∴∠1=∠2．
∵△DEF与△ADG都是等腰直角三角形，
∴∠DEF=∠DGA=45°，
∴∠CEF=∠FGH=135°，
在△CEF和△FGH中，

∵，

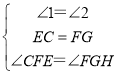∴△CEF≌△FGH(ASA)，
∴CF=FH；
(2)如图3，

∴∠DFE=∠DEF=45°，
∵AC=BC，∠ACB=90°，
∴∠A=∠CBA=45°，
∵线段DE绕点D逆时针旋转90°得到线段DF，

∴∠EDF=90°，ED=FD，

∴DF∥BC，
∴∠CBA=∠FGB=45°，∠DFC=∠FCB，
∴∠FGH=∠CEF=45°，
∵点D为AC的中点，DF∥BC，
∴DG=BC，DC=AC，
∴DG=DC，
∴ED- DC =FD-DG，

∴EC=GF，
∵∠DFC=∠FCB，∠ECB=∠CFH=90，

∴∠DFC+∠CFH=∠FCB+∠ECB，
∴∠GFH=∠ECF，
在△FCE和△HFG中，

∵，
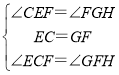∴△FCE≌△HFG(ASA)，
∴HF=FC，
∵∠EDF=90°，DE=DF，
∴∠DEF=∠DFE=45°，
∵∠CFE=15°，
∴∠DFC=45°-15°=30°，
∴CF=2CD，DF=CD，
∵DE=DF，CE=．
∴+CD=CD，
解得：CD=，
∴CF=2CD=．
∵∠CFH=90°，
∴△FCH的面积为：．