Question

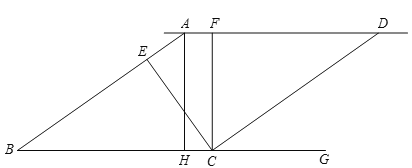
【题目】如图，矩形ABCD中，，点E在AD上，且，连接EC，将矩形ABCD沿直线BE翻折，点A恰好落在EC上的点A'处，则____________cm．

Answer 1

【答案】8

【解析】

设A′C=xcm，先根据已知利用AAS证明△A′BC≌△DCE，得出A′C=DE= xcm，则BC=AD=（9+x）cm，A′B=AB=15cm，然后在Rt△A′BC中，由勾股定理可得BC2=A′B2+A′C2，即可得方程，解方程即可求得答案

解：∵四边形ABCD是矩形，
∴AB=CD=15cm，∠A=∠D=90°，AD∥BC，AD=BC，
∴∠DEC=∠A′CB，
由折叠的性质，得：A′B=AB=15cm，∠BA′E=∠A=90°，
∴A′B=CD，∠BA′C=∠D=90°，
在△A′BC和△DCE中，

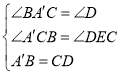
∴△A′BC≌△DCE（AAS），
∴A′C=DE，
设A′C=xcm，则BC=AD=DE+AE=x+9（cm），
在Rt△A′BC中，BC2=A′B2+A′C2，
即（x+9）2=x2+152，
解得：x=8，
∴A′C=8cm．
故答案为：8．