题目内容
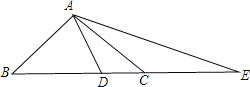
【题目】如图，在ABCD中，延长CD到E，使DE=CD，连接BE交AD于点F，交AC于点G．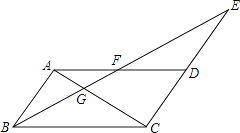
（1）求证：AF=DF；
（2）若BC=2AB，DE=1，∠ABC=60°，求FG的长．
【答案】
（1）
证明：连接BD、AE，
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵DE=CD，
∴AB∥DE，AB=DE，
∴四边形ABDE是平行四边形，
∴AF=DF．
（2）
解：在BC上截取BN=AB=1，连接AN，
∵∠ABC=60°，
∴△ANB是等边三角形，
∴AN=1=BN，∠ANB=∠BAN=60°，
∵BC=2AB=2，
∴CN=1=AN，
∴∠ACN=∠CAN= 
×60°=30°，
∴∠BAC=90°，
由勾股定理得：AC= 
= 
，
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴△AGB∽△CGE，
∴ 
，
∴ 
= 
，
AG= 
，
在△BGA中，由勾股定理得：BG= 
= 
，
∵ 
= ，
∴GE= 
，
BE= + =2 ，
∵四边形ABDE是平行四边形，
∴BF= BE= ，
∴FG= ﹣ = ．
【解析】（1）连接AE、BD、根据AB∥CD，AB=CD=DE，得出平行四边形ABDE，即可推出答案；（2）在BC上截取BN=AB=1，连接AN，推出△ANB是等边三角形，求出CN=1=AN，根据三角形的内角和定理求出∠BAC=90°，由勾股定理求出AC，根据△AGB∽△CGE，得出 ，求出AG，在△BGA中，由勾股定理求出BG，求出GE、BE，根据平行四边形BDEA求出BF，即可求出答案．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三的一半，以及对平行四边形的性质的理解，了解平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
