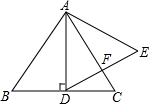
题目内容
已知:点P是等边△ABC内任意一点,它到三边的距离分别为h1、h2、h3,且满足h1+h2+h3=6,则S△ABC=______.
如图,在等边△ABC中,AB=BC=AC,
过点A作AD⊥BC,垂足为D,
则BD=CD=
BC=
AB,
∵S△ABC=
AB•h1+
BC•h2+
AC•h3=
BC•AD,
∴AD=h1+h2+h3=6,
在Rt△ABD中,AB2=BD2+AD2,
即AB2=(
AB)2+62,
AB=4
,
∴S△ABC=
BC•AD=
×4
×6=12
.
故答案为:12
.
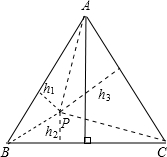
过点A作AD⊥BC,垂足为D,
则BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=h1+h2+h3=6,
在Rt△ABD中,AB2=BD2+AD2,
即AB2=(
| 1 |
| 2 |
AB=4
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:12
| 3 |


练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 C、AD.
C、AD.