题目内容
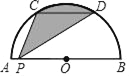
【题目】如图,C,D是以AB为直径的半圆周的三等分点,CD=8cm,P是直径AB上的任意一点.
(1)求![]() 的长;
的长;
(2)求阴影部分的面积.
【答案】(1)![]() ;(2)
;(2)![]() cm2.
cm2.
【解析】
连接OC、OD,根据C,D是以AB为直径的半圆周的三等分点,可得∠COD=60°,△OCD是等边三角形,即可根据弧长公式求出![]() 的长,将阴影部分的面积转化为扇形OCD的面积求解即可.
的长,将阴影部分的面积转化为扇形OCD的面积求解即可.
解:(1)如图,连接OC、OD.
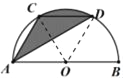
∵C,D是以AB为直径的半圆周的三等分点,
∴∠AOC=∠COD=∠DOB=60°,
又∵OC=OD,
∴△OCD是等边三角形,
∴OC=CD=8,
∴![]() 的长=
的长=![]() =
=![]() cm;
cm;
(2)∵∠OCD=∠AOC=60°
∴CD∥AB,
∴S△ACD=S△OCD,
∴S阴影=S扇形OCD=![]() =
=![]() .
.
故答案为:(1)![]() ;(2)
;(2)![]() cm2.
cm2.

练习册系列答案
相关题目