题目内容
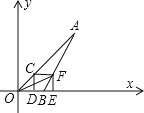
【题目】如图示意图,A点的坐标为(2,2),点C在线段OA上运动(点C不与O、A重合),过点C作CD⊥x轴于D,再以CD为一边在CD右侧画正方形CDEF.连接AF并延长交x轴于B,连接OF.若△BEF与△OEF相似,则点B的坐标是________.

【答案】(1,0)(3,0)(6,0)
【解析】
设![]() ,依题意要使△BEF∽△OFE,则要
,依题意要使△BEF∽△OFE,则要![]() 或
或![]()
即分BE=2t或![]() 两种情况解答.当BE=2t时,BO=4t,根据上述的线段比求出t值;当
两种情况解答.当BE=2t时,BO=4t,根据上述的线段比求出t值;当![]() 时也要细分两种情况:当B在E的右侧以及当B在E的左侧时OB的取值,利用线段比求出t值.
时也要细分两种情况:当B在E的右侧以及当B在E的左侧时OB的取值,利用线段比求出t值.
设![]()
∵A(2,2),
∴![]()
∴CD=OD=DE=EF=t,
∵CF∥OB,
∴△ACF∽△AOB,
∴![]()
∴![]()
要使△BEF与△OFE相似,
∵![]()
∴只要![]() 或
或![]()
即:BE=2t或![]() ,
,
①当BE=2t时,BO=4t,
∴![]()
∴t1=0(舍去)或![]() ,
,
∴B(6,0).
②当![]() 时,
时,
(ⅰ)当B在E的左侧时,
![]()
∴![]()
∴t1=0(舍去)或![]()
∴B(1,0).
(ⅱ)当B在E的右侧时,![]()
∴![]()
∴t1=0(舍去)或![]()
∴B(3,0).
综上,B(1,0)(3,0)(6,0).
故答案为:(1,0)(3,0)(6,0).

练习册系列答案
相关题目