题目内容
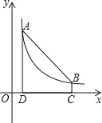
【题目】如图,点A(m,4),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=3,在x轴上存在一点P,使|PA﹣PB|的值最大,则P点的坐标是( )
A. (5,0)B. (4.0)C. (3,0)D. (2,0)
【答案】A
【解析】
根据题意列出关于m、n的方程组,得到m、n的值,求出反比例函数解析式,由三角形三边关系可知,当A、B、P在同一条直线上时,|PA﹣PB|最大,求出直线AB的解析式,即可得到P点坐标.
设反比例函数的表达式为y=![]() ,
,
∵A(m,4),B(n,1)在反比例函数上,
∴4m=n,
∵DC=3,
∴n﹣m=3,
解得:m=1,n=4,
∴A(1,4),B(4,1)
把A(1,4)代入y=![]() 中,
中,
解得:k=4
∴反比例函数表达式为y=![]() .
.
由三角形三边关系,两边之差小于第三边可得,|PA﹣PB|<AB,
所以当A、B、P在同一条直线上时,PA﹣PB=AB时,|PA﹣PB|最大.
设直线AB的解析式为y=kx+b
将A(1,4),B(4,1)代入解析式可得:k=﹣1,b=5
所以直线AB的解析式为y=﹣x+5,
∵P在x轴上,当y=0时,x=5,
∴P(5,0).
故选:A.

练习册系列答案
相关题目
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?