题目内容
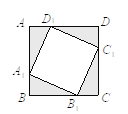
【题目】如右图,把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得正方形A1B1C1D1,且剩下图形的面积为原正方形面积的![]() ,则AA1=_____.
,则AA1=_____.
【答案】![]() 或
或![]()
【解析】
本题中易证四边的四个小直角三角形全等,那么可设一边为x,那么另一边就是(1-x),可用勾股定理求出里面的正方形的边长的平方也就是其面积,然后根据剩下图形的面积为原来正方形面积的![]() ,来列方程求解.
,来列方程求解.
解:∵A1B1C1D1是正方形,
∴A1B1=B1C1=C1D1=D1A1,
∵∠AA1D1+∠AD1A1=90°,∠AA1D1+∠BA1B1=90°,
∴∠AD1A1=∠BA1B1,
同理可得:∠AD1A1=∠BA1B1=∠DC1D1=∠C1B1C,
∵∠A=∠B=∠C=∠D,
∴△AA1D1≌△BB1A1≌△CC1B1≌△DD1C1,
∴AA1=D1D,
设AD1=x,那么AA1=DD1=1-x,
Rt△AA1D1中,根据勾股定理可得:
A1D12=x2+(1-x)2,
∴正方形A1B1C1D1的面积=A1D12=x2+(1-x)2=![]() ,
,
解得x=![]() 或
或![]() .
.
∴AA1=1-x=![]()
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40