题目内容
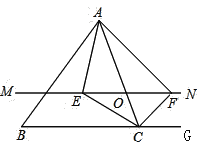
【题目】如图,一个三角形的纸片ABC,其中∠A=∠C,
(1)把△ABC纸片按 (如图1) 所示折叠,使点A落在BC边上的点F处,DE是折痕.说明 BC∥DF;
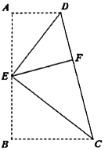
(2)把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
(3)当点A落在四边形BCED外时 (如图3),探索∠C与∠1、∠2之间的大小关系.(直接写出结论)

【答案】(1)见解析;(2)∠1+∠2=2∠C;(3)∠1-∠2=2∠C.
【解析】
(1)根据折叠的性质得∠DFE=∠A,由已知得∠A=∠C,于是得到∠DFE=∠C,即可得到结论;
(2)先根据四边形的内角和等于360°得出∠A+∠A′=∠1+∠2,再由图形翻折变换的性质即可得出结论;
(3)∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β),于是得到∠2+2α=180°,∠1=β-∠BDE=β-(∠A+α),推出∠2-∠1=180°-(α+β)+∠A,根据三角形的内角和得到∠A=180°-(α+β),证得∠2-∠1=2∠A,于是得到结论.
解:(1) 由折叠知∠A=∠DFE,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
(2)∠1+∠2=2∠A.理由如下:
∵∠1+2∠AED=180°, ∠2+2∠ADE=180°,
∴∠1+∠2+2(∠ADE+∠AED)=360°.
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-∠A,
∴∠1+∠2+2(180°-A)=360°,
即∠1+∠2=2∠C.
(3)∠1-∠2=2∠A.
∵2∠AED+∠1=180°,2∠ADE-∠2=180°,
∴2(∠ADE+∠AED)+∠1-∠2=360°.
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-∠A,
∴∠1-∠2+2(180°-∠A)=360°,
即∠1-∠2=2∠C.