[题目]如图.四边形中...为上一点.分别以.为折痕将两个角(.)向内折起.点.恰好都落在边的点处．若..则．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，四边形中，，，为上一点，分别以，为折痕将两个角（，）向内折起，点，恰好都落在边的点处．若，，则________．

【答案】

【解析】

先根据折叠的性质得EA=EF，BE=EF，DF=AD=3，CF=CB=5，则AB=2EF，DC=8，再作DH⊥BC于H，由于AD∥BC，∠B=90°，则可判断四边形ABHD为矩形，所以DH=AB=2EF，HC=BC-BH=BC-AD=2，然后在Rt△DHC中，利用勾股定理计算出DH=，所以EF=.

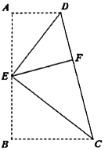
解：∵分别以ED，EC为折痕将两个角（∠A，∠B）向内折起，点A，B恰好落在CD边的点F处，
∴EA=EF，BE=EF，DF=AD=3，CF=CB=5，
∴AB=2EF，DC=DF+CF=8，
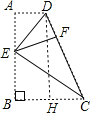
作DH⊥BC于H，
∵AD∥BC，∠B=90°，
∴四边形ABHD为矩形，
∴DH=AB=2EF，HC=BC-BH=BC-AD=5-3=2，
在Rt△DHC中，DH=，

∴EF=DH=.

故答案为：.

练习册系列答案

相关题目

【题目】如图，边长为2的正方形ABCD内接于⊙O，过点D作⊙O的切线交BA延长线于点E，连接EO，交AD于点F，则EF长为．

【题目】如图，一个三角形的纸片ABC，其中∠A=∠C,

（1）把△ABC纸片按 (如图1) 所示折叠，使点A落在BC边上的点F处，DE是折痕．说明 BC∥DF；

（2）把△ABC纸片沿DE折叠，当点A落在四边形BCED内时 (如图2)，探索∠C与∠1+∠2之间的大小关系，并说明理由；

（3）当点A落在四边形BCED外时 (如图3)，探索∠C与∠1、∠2之间的大小关系.(直接写出结论)

【题目】（1）如图1，等腰和等腰中，，，，三点在同一直线上，求证：；

（2）如图2，等腰中，，，是三角形外一点，且，求证：；

（3）如图3，等边中，是形外一点，且，

①的度数为；

②，，之间的关系是 .

【题目】已知如图抛物线y=ax2+bx+c与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C（0，﹣3）

（1）请直接写出抛物线的解析式．
（2）抛物线的对称轴上是否存在一点P，使得△ACP的周长最短，若存在，请直接写出点P的坐标．
（3）点G的坐标是（2，﹣3），点F是x轴上一点，抛物线上是否存在点R，使得以A，G，F，R为顶点的四边形是平行四边形？若存在，直接写出点R的坐标．
（4）在B、C连线的下方抛物线上是否存在一点Q，使得△QBC的面积是△ABC的面积的一半？若存在，求出点Q的坐标．
（5）抛物线的顶点设为D，对称轴与y轴的交点为E，M（m，0）是x轴上一动点，点N是线段DE上的一点，若∠MNC=90°，请直接写出实数m的变化范围．