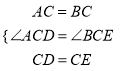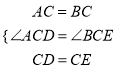题目内容
【题目】如图,已知平行于y轴的动直线a的表达式为x=t,直线b的表达式为y=x,直线c的表达式为y=﹣![]() x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.
x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.

【答案】![]() ,
, ![]() ,
, ![]() ,
, ![]()
【解析】解:∵当x=t时,y=x=t;当x=t时,y=﹣![]() x+2=﹣
x+2=﹣![]() t+2,∴E点坐标为(t,﹣
t+2,∴E点坐标为(t,﹣![]() t+2),D点坐标为(t,t).
t+2),D点坐标为(t,t).
∵E在D的上方,∴DE=﹣![]() t+2﹣t=﹣
t+2﹣t=﹣![]() t+2,且t<
t+2,且t<![]() .
.
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
t>0时,PE=DE时,﹣![]() t+2=t,∴t=
t+2=t,∴t=![]() ,﹣
,﹣![]() t+2=
t+2=![]() .∴P点坐标为(0,
.∴P点坐标为(0, ![]() ).
).
①若t>0,PD=DE时,﹣![]() t+2=t,∴t=
t+2=t,∴t=![]() .∴P点坐标为(0,
.∴P点坐标为(0, ![]() );
);
②若t>0,PE=PD时,即DE为斜边,∴﹣ ![]() t+2=2t,∴t=
t+2=2t,∴t=![]() ,DE的中点坐标为(t,
,DE的中点坐标为(t, ![]() t+1),∴P点坐标为(0,
t+1),∴P点坐标为(0, ![]() );
);
若t<0,PE=DE和PD=DE时,由已知得DE=﹣t,﹣ ![]() t+2=﹣t,t=4>0(不符合题意,舍去),此时直线x=t不存在;
t+2=﹣t,t=4>0(不符合题意,舍去),此时直线x=t不存在;
③若t<0,PE=PD时,即DE为斜边,由已知得DE=﹣2t,﹣ ![]() t+2=﹣2t,∴t=﹣4,
t+2=﹣2t,∴t=﹣4, ![]() t+1=0,∴P点坐标为(0,0).
t+1=0,∴P点坐标为(0,0).
综上所述: P点坐标为(0, ![]() )或(0,
)或(0, ![]() )或(0,
)或(0, ![]() )或(0,0).
)或(0,0).

练习册系列答案
相关题目