题目内容
【题目】在平面直角坐标系中,有点
，且在
轴上有另一点
,使 三角形
的面积为
，则点坐标为__________．
【答案】(2,0)或(-2,0).
【解析】
设A，B所在的直线的解析式为y=kx+b，根据A，B 的坐标求出该解析式，然后设点P到y轴的距离为
，根据A，B的位置分情况计算
即可得出P点坐标.
解：设A，B所在的直线的解析式为y=kx+b
把
代入，得
解得
∴A，B所在的直线的解析式为y=2x
∴A，B，O在同一直线上
设点P到y轴的距离为
①
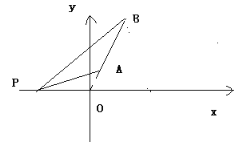
如上图所示：
=
=
=
=2
∵
∴2=4
∴
∴点P坐标为(2,0)或(-2,0)
②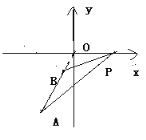
如上图：
=
=
=
=2
∵
∴2=4
∴
∴点P坐标为(2,0)或(-2,0)
③
如上图所示：
=
=
=
=2
∵
∴2=4
∴
∴点P坐标为(2,0)或(-2,0)
综上所述，点P坐标为(2,0)或(-2,0).
故答案为(2,0)或(-2,0).
【题目】某数码专营店销售甲、乙两种品牌智能手机，这两种手机的进价和售价如下表所示：
甲 | 乙 | |
进价（元/部） | 4300 | 3600 |
售价（元/部） | 4800 | 4200 |
（1）该店销售记录显示．三月份销售甲、乙两种手机共17部，且销售甲种手机的利润恰好是销售乙种手机利润的2倍，求该店三月份售出甲种手机和乙种手机各多少部？
（2）根据市场调研，该店四月份计划购进这两种手机共20部，要求购进乙种手机数不超过甲种手机数的
，而用于购买这两种手机的资金低于81500元，请通过计算设计所有可能的进货方案．
（3）在（2）的条件下，该店打算将四月份按计划购进的20部手机全部售出后，所获得利润的30%用于购买A，B两款教学仪器捐赠给某希望小学．已知购买A仪器每台300元，购买B仪器每台570元，且所捐的钱恰好用完，试问该店捐赠A，B两款仪器一共多少台？（直接写出所有可能的结果即可）
【题目】某批发商计划将一批海产品由A地运往B地．汽车货运公司和铁路货运公司均开办海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米／时、100千米／时．两货运公司的收费项目及收费标准如下表所示：
运输工具 | 运输费单价／ (元／吨·千米) | 冷藏费单价／ (元／吨·小时) | 过路费／元 | 装卸及管理费／元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注：“元／吨·千米”表示每吨货物每千米的运费；“元／吨·小时”表示每吨货物每小时的冷藏费．
(1)设该批发商待运的海产品有x(吨)，汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元)，试求y1、y2与x之间的函数关系式．
(2)若该批发商待运的海产品不少于30吨，为节省运费，他应选择哪个货运公司承担运输业务?
