Question

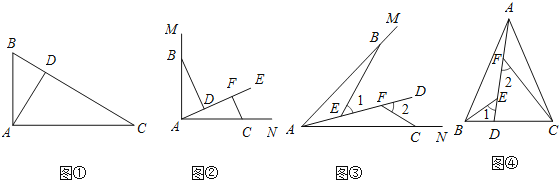
【题目】如图,在三角形中, ,点是上一点,点是三角形外上一点, 且点为线段上一点，连接，且．

（1）若，求的度数；

（2）若，求的度数

Answer 1

【答案】（1）110°；（2）80°.

【解析】

（1）根据∠A=∠ACE得到AB∥CE，根据平行线的性质得到∠B+∠BCE=180°，从而得到的度数；

（2）根据得到∠E+∠BCE=180°，因为，所以得到∠DCE=40°，所以可以求出∠BCE=∠DCE=×40°=100°，由（1）知∠B+∠BCE=180°，所以∠B=180°-100°=80°.

解：（1）∵，

∴∠A=∠ACE

∴AB∥CE

∴∠B+∠BCE=180°

∵

∴=180°-70°=110°

（2）∵

∴∠E+∠BCE=180°

∵∠E=2∠DCE

∴2∠DCE+∠BCE=180°

∵2∠BCD=3∠DCE，∠BCE=∠BCD+∠DCE

∴∠BCE=∠DCE+∠DCE=∠DCE

∴2∠DCE+∠DCE=180°

∴∠DCE=40°

∴∠BCE=∠DCE=×40°=100°

由（1）知∠B+∠BCE=180°

∴∠B=180°-100°=80°

故答案为（1）110°；（2）80°.