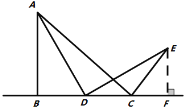
题目内容
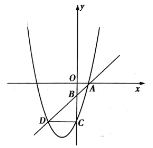
【题目】如图，在
中，
，
为
边上的中线,
于点
（1）求证：BD·AD=DE·AC.
（2）若AB=13,BC=10,求线段DE的长.
（3）在（2）的条件下，求
的值.
【答案】（1）见解析；（2）
；（3）
.
【解析】
（1）先利用等腰三角形的性质证明∠B=∠C，AD⊥BC，然后再证明△BDE∽△CAD即可；
（2）利用勾股定理求出AD，再根据（1）的结论即可求出DE；
（3）在Rt△BDE中，利用锐角三角函数求解即可.
解：（1）证明：∵AB=AC， AD为BC边上的中线，
∴∠B=∠C，AD⊥BC，即∠ADC=90°，
又∵DE⊥AB于点E，即∠DEB=90°，
∴∠ADC=∠DEB，
∴△BDE∽△CAD，
∴
，
∴BD·AD=DE·AC；
（2）∵AD为BC边上的中线，BC=10，
∴BD=CD=5，
在Rt△ABD中，AB=13，BD=5，
∴AD= 
，
由（1）得BD·AD=DE·AC，
又∵AC=AB= 13，
∴5×12=13·DE，
∴DE=
；
（3）由（2）知，DE=，BD=5，
∴在Rt△BDE中，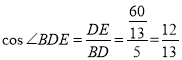
.
练习册系列答案
相关题目
【题目】为了解我市居民用水情况，在某小区随机抽查了20户家庭，并将这些家庭的月用水量进行统计，结果如下表：
月用水量（吨） | 4 | 5 | 6 | 8 | 13 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量，下列说法正确的是（ ）
A.中位数是5B.平均数是5C.众数是6D.方差是6
