题目内容
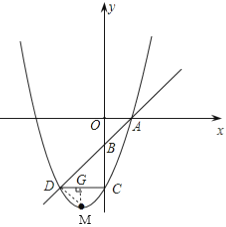
【题目】如图，一次函数y=x+m图象过点A(1，0)，交y轴于点
，
为y轴负半轴上一点，且
，过
、两点的抛物线交直线
于点
，且CD//x轴．
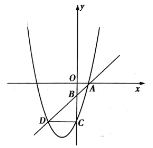
（1）求这条抛物线的解析式；
（2）观察图象，写出使一次函数值小于二次函数值时
的取值范围；
（3）在题中的抛物线上是否存在一点
，使得
为直角？若存在，求出点的坐标；若不存在，请说明理由．
【答案】（1）y=x2+2x-3；（2）x<-2或x>1；（3）存在，M（-1，-4）.
【解析】
（1）把A点坐标代入y=x+m可求出m的值，可得一次函数解析式，即可得点B坐标，根据BC=2OB可求出C点坐标，根据CD//x轴可求出D点坐标，设抛物线的解析式为y=ax2+bx+c，利用待定系数法求出a、b、c的值即可得答案；（2）根据A、D两点坐标，找出一次函数图象在二次函数图象下方的x的取值范围即可；（3）过D作DM⊥AD，交抛物线于M，过M作MG⊥CD于G，设E（t，t2+2t-3），根据B、C、D三点坐标可得△BCD是等腰直角三角形，进而可证明△DMG是等腰直角三角形，用t表示出DG和MG的长，利用DG=MG列方程求出t的值即可得答案.
（1）∵点A（1，0）在一次函数y=x+m图象上，
∴1+m=0，
∴m=-1，
∴直线AB的解析式为：y=x-1，
当x=0时，y=-1，
∴点B坐标为：（0，-1），
∴OB=1，
∵
为y轴负半轴上一点，且
，
∴BC=2，OC=3，
∴点C坐标为：（0，-3），
∵CD//x轴，点D在直线AB上，
∴当y=-3时，x-1=-3，
解得x=-2，
∴点D坐标为：（-2，-3），
设这条抛物线的解析式为y=ax2+bx+c，
∵抛物线结果A、C、D三点，
∴
，
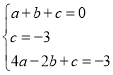解得：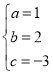
，
∴这条抛物线的解析式为：y=x2+2x-3.
（2）∵一次函数值小于二次函数值，
∴一次函数图象在二次函数图象下方，
∵一次函数与二次函数交于A（1，0）、D（-2，-3），
∴x<-2或x>1.
（3）如图，过D作DM⊥AD，交抛物线于M，过M作MG⊥CD于G，设M（t，t2+2t-3），
∵C（0，-3），D（-2，-3），
∴CD=2，
∴BC=CD=2，
∵CD//x轴，
∴∠BCD=90°，
∴△BCD是等腰直角三角形，
∴∠BDC=45°，
∵DM⊥AD，
∴∠ADM=90°，
∴∠CDM=90°-45°=45°，
∵MG⊥CD，
∴△DMG是等腰直角三角形，
∴DG=CG，
∵CD//x轴，C(0，-3)，
∴点G坐标为（t，-3），
∴DG=t+2，MG=-3-（t2+2t-3）=-t2-2t，
∴-t2-2t=t+2，
解得：t=-1或t=-2，
∵t=-2时，点M与点D重合，
∴t=-1，
∴t2+2t-3=-4，
∴点M坐标为（-1，-4），
∴存在一点M，使得
为直角，点M的坐标为（-1，-4）.
