题目内容
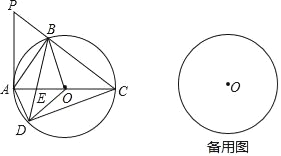
【题目】如图,已知一次函数y=![]() x3与反比例函数y=
x3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=![]() 的图象,当y2时,请直接写出自变量x的取值范围。
的图象,当y2时,请直接写出自变量x的取值范围。
【答案】(1)n=3,k=12;(2)(4+![]() ,3);(3)x6或x>0.
,3);(3)x6或x>0.
【解析】
(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=
x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
(3)根据反比例函数的性质即可得到当y≥-2时,自变量x的取值范围.
(1)把点A(4,n)代入一次函数y=![]() x3,可得n=
x3,可得n=![]() ×43=3;
×43=3;
把点A(4,3)代入反比例函数y=![]() ,可得3=
,可得3=![]() ,
,
解得k=12.
(2)∵一次函数y=![]() x3与x轴相交于点B,
x3与x轴相交于点B,
∴![]() x3=0,
x3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,

过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OEOB=42=2,
在Rt△ABE中,
AB=![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC=![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+![]() +2=4+
+2=4+![]() ,
,
∴点D的坐标为(4+![]() ,3).
,3).
(3)当y=2时,2=![]() ,解得x=6.
,解得x=6.
故当y2时,自变量x的取值范围是x6或x>0.