题目内容
【题目】完成下面的证明(在括号中填写推理理由) 如图,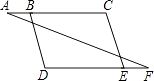
已知∠A=∠F,∠C=∠D,求证:BD∥CE.
证明:因为∠A=∠F,
所以AC∥DF(),
所以∠C+∠=180°().
因为∠C=∠D,
所以∠D+∠=180°(),
所以BD∥CE().
【答案】内错角相等,两直线平行;CED;两直线平行,同旁内角互补;CED;等量代换;同旁内角互补,两直线平行
【解析】证明:∵∠A=∠F, ∴AC∥DF(内错角相等,两直线平行),
∴∠C+∠CED=180°(两直线平行,同旁内角互补).
∵∠C=∠D,
∴∠D+∠CDE=180°(等量代换),
∴BD∥CE(同旁内角互补,两直线平行),
所以答案是:内错角相等,两直线平行,CED,两直线平行,同旁内角互补,CED,等量代换,同旁内角互补,两直线平行.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

