题目内容
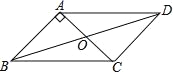
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.
【答案】(1)S□ABCD=2,(2)BD=![]()
【解析】试题分析:(1)在Rt△ABC中利用勾股定理求出AC的长,然后利用平行四边形的面积公式计算即可;(2)在Rt△AOB中利用勾股定理求出BO的长,在利用平行四边形的性质可得BD=2 BO=![]() .
.
试题解析:(1)因为AB⊥AC,AB=1,BC=![]() ,所以AC=
,所以AC=![]() ,所以S□ABCD;=AC.BC=2;
,所以S□ABCD;=AC.BC=2;
(2)因为四边形ABCD是平行四边形,∴AO=OC=1,BO=DO,在Rt△AOB中由勾股定理可得: ![]() ,所以BD=2 BO=
,所以BD=2 BO=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目