题目内容
【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

【答案】(1)∠AOF=∠COF,理由详见解析;(2)∠BOE=120°.
【解析】
(1)求出∠AOD度数,求出∠AOE,求出∠AOF,即可得出答案;
(2)求出∠BOD度数,求出∠DOE度数,相加即可得出答案.
(1)答:∠AOF=∠COF,
证明:∵O是直线CD上一点,
∴∠AOC+∠AOD=180°,
∵∠AOC=60°,
∴∠AOD=180°﹣60°=120°,
∵OE平分∠AOD,
∴![]() .
.
∵OF⊥OE,
∴∠FOE=90°
∴∠AOF=∠FOE﹣∠AOE=90°﹣60°=30°,
∴∠COF=∠AOC﹣∠AOF=60°﹣30°=30°,
∴∠AOF=∠COF.
(2)解:∵∠AOC=60°,
∴∠BOD=∠AOC=60°,∠AOD=180°﹣60°=120°,
∵OE是∠AOD的平分线,
∴∠DOE=![]() ∠AOD=60°,
∠AOD=60°,
∴∠BOE=∠BOD+∠DOE=60°+60°=120°.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
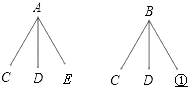
(1)下列是该店用树形图或列表设计的配套方案,①的位置应填写 , ②的位置应 填写
(2)若仅有B型打印机与E种芯片不配套,则上面(1)中的方案配套成功率是
芯片 | C | D | E |
A | (A,C) | (A,D) | ② |
B | (B,C) | (B,D) | (B,E) |