题目内容
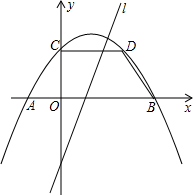 如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2, )在抛物线上,直线l是一次函数y=kx-2(k≠0)的图象,点O是坐标原点.
)在抛物线上,直线l是一次函数y=kx-2(k≠0)的图象,点O是坐标原点.
(1)求抛物线的解析式;
(2)若直线l平分四边形OBDC的面积,求k的值;
(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线l交于M,N两点,问在y轴正半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.
 解:(1)因为抛物线关于直线x=1对称,AB=4,所以A(-1,0),B(3,0),
解:(1)因为抛物线关于直线x=1对称,AB=4,所以A(-1,0),B(3,0),设抛物线的解析式为y=a(x+1)(x-3),
∵点D(2,
 )在抛物线上,
)在抛物线上,∴
 =a×3×(-1),解得a=
=a×3×(-1),解得a= ,
,∴抛物线解析式为:y=
 (x+1)(x-3)=
(x+1)(x-3)= x2+x+
x2+x+ .
.(2)抛物线解析式为:y=
 x2+x+
x2+x+ ,令x=0,得y=
,令x=0,得y= ,∴C(0,
,∴C(0, ),
),∵D(2,
 ),∴CD∥OB,直线CD解析式为y=
),∴CD∥OB,直线CD解析式为y= .
.直线l解析式为y=kx-2,令y=0,得x=
 ;令y=
;令y= ,得x=
,得x= ;
;如答图1所示,设直线l分别与OB、CD交于点E、F,则E(
 ,0),F(
,0),F( ,
, ),
),OE=
 ,BE=3-
,BE=3- ,CF=
,CF= ,DF=2-
,DF=2- .
.∵直线l平分四边形OBDC的面积,
∴S梯形OEFC=S梯形FDBE,
∴
 (OE+CF)•OC=
(OE+CF)•OC= (FD+BE)•OC,
(FD+BE)•OC,∴OE+CF=FD+BE,即:
 +
+ =(3-
=(3- )+(2-
)+(2- ),
),解方程得:k=
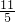 ,经检验k=
,经检验k=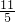 是原方程的解且符合题意,
是原方程的解且符合题意,∴k=
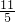 .
.(3)假设存在符合题意的点P,其坐标为(0,t).

抛物线解析式为:y=
 x2+x+
x2+x+ =
= (x-1)2+2,
(x-1)2+2,把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线解析式为:y=
 x2.
x2.依题意画出图形,如答图2所示,过点M作MD⊥y轴于点D,NE⊥y轴于点E,
设M(xm,ym),N(xn,yn),则MD=-xm,PD=t-ym;NE=xn,PE=t-yn.
∵直线PM与PN关于y轴对称,∴∠MPD=∠NPE,
又∠MDP=∠NEP=90°,
∴Rt△PMD∽Rt△PNE,
∴
 ,即
,即 ①,
①,∵点M、N在直线y=kx-2上,∴ym=kxm-2,yn=kxn-2,
代入①式化简得:(t+2)(xm+xn)=2kxmxn ②
把y=kx-2代入y=
 x2.,整理得:x2+2kx-4=0,
x2.,整理得:x2+2kx-4=0,∴xm+xn=-2k,xmxn=-4,代入②式解得:t=2,符合条件.
所以在y轴正半轴上存在一个定点P(0,2),使得不论k取何值,直线PM与PN总是关于y轴对称.
分析:(1)首先求出点A、B的坐标,然后利用交点式、待定系数法求出抛物线的解析式;
(2)首先求出点C坐标,确定CD∥OB;由题意,直线l平分四边形OBDC的面积,则S梯形OEFC=S梯形FDBE,据此列方程求出k的值;
(3)首先求出平移变换后的抛物线解析式,如答图2所示,然后证明Rt△PMD∽Rt△PNE,由相似三角形比例线段关系得到式①:
 ,化简之后变为式②:(t+2)(xm+xn)=2kxmxn;最后利用一元二次方程根与系数的关系求出t的值.
,化简之后变为式②:(t+2)(xm+xn)=2kxmxn;最后利用一元二次方程根与系数的关系求出t的值.点评:本题是二次函数综合题,考查了二次函数的图象与性质、待定系数法、抛物线的平移、相似三角形、一元二次方程根与系数关系、图形面积计算等知识点,有一定的难度.第(2)问的解题要点是根据S梯形OEFC=S梯形FDBE(如答图1)列方程求解,第(3)问是存在型问题,综合利用相似三角形的判定与性质、函数图象上点的坐标特征及一元二次方程根与系数关系求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
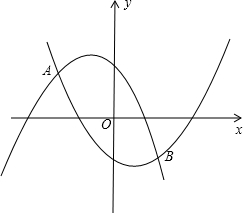 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?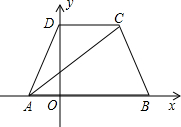 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.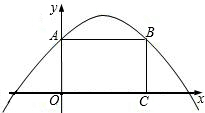 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,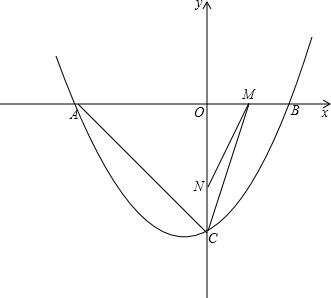 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).