题目内容
已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
(1)求证:平行四边形ABFC是平行四边形;
(2)若BC⊥AB,且BC=12,AB=8,求AF的长.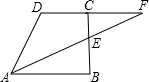
(1)求证:平行四边形ABFC是平行四边形;
(2)若BC⊥AB,且BC=12,AB=8,求AF的长.

(1)证明:∵E为BC的中点,
∴BE=CE,
∵AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AE=FE,
又∵在四边形ABFC中,BE=CE,
∴四边形ABFC是平行四边形;
(2)∵BC=12,E是BC的中点,
∴BE=
BC=
×12=6,
∵BC⊥AB,
∴AE=
=
=10,
∴AF=2AE=2×10=20.
∴BE=CE,
∵AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
在△ABE和△FCE中,
|
∴△ABE≌△FCE(AAS),
∴AE=FE,
又∵在四边形ABFC中,BE=CE,
∴四边形ABFC是平行四边形;
(2)∵BC=12,E是BC的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∵BC⊥AB,
∴AE=
| AB2+BE2 |
| 82+62 |
∴AF=2AE=2×10=20.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )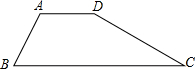 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=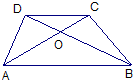 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.