题目内容
如图，矩形ABCD，E为BC边上一点，将△ABE沿AE对折，使点B的对应点F落在边DC上，若∠DAF=20°，则∠FBE的度数是（ ）
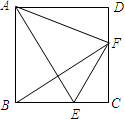
| A．20° | B．25° | C．35° | D．40° |
∵四边形ABCD是矩形，
∴∠BAD=∠ABC=90°，
∴∠ABF+∠FBE=90°，
由折叠的性质可得：∠BAE=∠FAE，∠BAE+∠ABF=90°，
∴∠FBE=∠BAE，
∵∠DAF=20°，
∴∠BAE=
=35°，
∴∠FBE=35°．
故选C．
∴∠BAD=∠ABC=90°，
∴∠ABF+∠FBE=90°，
由折叠的性质可得：∠BAE=∠FAE，∠BAE+∠ABF=90°，
∴∠FBE=∠BAE，
∵∠DAF=20°，
∴∠BAE=
| 90°-20° |
| 2 |
∴∠FBE=35°．
故选C．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
