题目内容
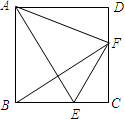
附图(①)为一张三角形ABC纸片,P点在BC上.今将A折至P时,出现折线BD,其中D点在AC上,如图(②)所示.若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为何?( )


| A.3:2 | B.5:3 | C.8:5 | D.13:8 |
由题意可得:S△ABD=S△ABC-S△DBC=80-50=30.
由折叠性质可知,S△DBP=S△ABD=30,
∴S△DCP=S△DBC-S△DBP=50-30=20.
∴BP:PC=S△DBP:S△DCP=30:20=3:2.
故选A.
由折叠性质可知,S△DBP=S△ABD=30,
∴S△DCP=S△DBC-S△DBP=50-30=20.
∴BP:PC=S△DBP:S△DCP=30:20=3:2.
故选A.

练习册系列答案
相关题目