题目内容
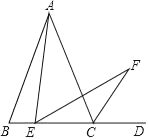
【题目】如图1，抛物线y=ax2+bx+4过A（2，0）、B（4，0）两点，交y轴于点C，过点C作x轴的平行线与抛物线上的另一个交点为D，连接AC、BC．点P是该抛物线上一动点，设点P的横坐标为m（m＞4）．
（1）求该抛物线的表达式和∠ACB的正切值；
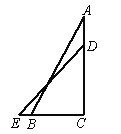
（2）如图2，若∠ACP=45°，求m的值；
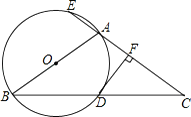
（3）如图3，过点A、P的直线与y轴于点N，过点P作PM⊥CD，垂足为M，直线MN与x轴交于点Q，试判断四边形ADMQ的形状，并说明理由．
【答案】（1）y=
x2﹣3x+4；tan∠ACB=
；（2）m=
；（3）四边形ADMQ是平行四边形；
【解析】
（1）由点A、B坐标利用待定系数法求解可得抛物线解析式为y=x2-3x+4，作BG⊥CA，交CA的延长线于点G，证△GAB∽△OAC得
=
，据此知BG=2AG．在Rt△ABG中根据BG2+AG2=AB2，可求得AG=
．继而可得BG=
，CG=AC+AG=
，根据正切函数定义可得答案；
（2）作BH⊥CD于点H，交CP于点K，连接AK，易得四边形OBHC是正方形，应用“全角夹半角”可得AK=OA+HK，设K（4，h），则BK=h，HK=HB-KB=4-h，AK=OA+HK=2+（4-h）=6-h．在Rt△ABK中，由勾股定理求得h=
，据此求得点K（4，）．待定系数法求出直线CK的解析式为y=-x+4．设点P的坐标为（x，y）知x是方程x2-3x+4=-x+4的一个解．解之求得x的值即可得出答案；
（3）先求出点D坐标为（6，4），设P（m，m2-3m+4）知M（m，4），H（m，0）．及PH=m2-3m+4），OH=m，AH=m-2，MH=4．①当4＜m＜6时，由△OAN∽△HAP知
=
．据此得ON=m-4．再证△ONQ∽△HMQ得
=
．据此求得OQ=m-4．从而得出AQ=DM=6-m．结合AQ∥DM可得答案．②当m＞6时，同理可得．
（1）将点A（2，0）和点B（4，0）分别代入y=ax2+bx+4，得
，
解得：
；
∴该抛物线的解析式为y=x2﹣3x+4，
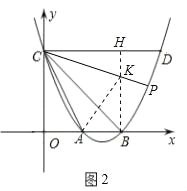
过点B作BG⊥CA，交CA的延长线于点G（如图1所示），则∠G=90°．
∵∠COA=∠G=90°，∠CAO=∠BAG，
∴△GAB∽△OAC．
∴
=2．
∴BG=2AG，
在Rt△ABG中，∵BG2+AG2=AB2，
∴（2AG）2+AG2=22，解得： AG=．
∴BG=，CG=AC+AG=2
+=．
在Rt△BCG中，tan∠ACB═
．
（2）如图2，过点B作BH⊥CD于点H，交CP于点K，连接AK．易得四边形OBHC是正方形．
应用“全角夹半角”可得AK=OA+HK，
设K（4，h），则BK=h，HK=HB﹣KB=4﹣h，AK=OA+HK=2+（4﹣h）=6﹣h，
在Rt△ABK中，由勾股定理，得AB2+BK2=AK2，
∴22+h2=（6﹣h）2．解得h=，
∴点K（4，），
设直线CK的解析式为y=hx+4，
将点K（4，）代入上式，得=4h+4．解得h=﹣，
∴直线CK的解析式为y=﹣x+4，
设点P的坐标为（x，y），则x是方程x2﹣3x+4=﹣x+4的一个解，
将方程整理，得3x2﹣16x=0，
解得x1=，x2=0（不合题意，舍去）
将x1=代入y=﹣x+4，得y=
，
∴点P的坐标为（，），
∴m=；
（3）四边形ADMQ是平行四边形．理由如下：
∵CD∥x轴，
∴yC=yD=4，
将y=4代入y=x2﹣3x+4，得4=x2﹣3x+4，
解得x1=0，x2=6，
∴点D（6，4），
根据题意，得P（m， m2﹣3m+4），M（m，4），H（m，0），
∴PH=m2﹣3m+4，OH=m，AH=m﹣2，MH=4，
①当4＜m＜6时，DM=6﹣m，
如图3，
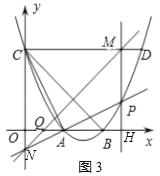
∵△OAN∽△HAP，
∴
，
∴
=
，
∴ON=
=
=m﹣4，
∵△ONQ∽△HMQ，
∴
，
∴
，
∴
，
∴OQ=m﹣4，
∴AQ=OA﹣OQ=2﹣（m﹣4）=6﹣m，
∴AQ=DM=6﹣m，
又∵AQ∥DM，
∴四边形ADMQ是平行四边形．
②当m＞6时，同理可得：四边形ADMQ是平行四边形．
综上，四边形ADMQ是平行四边形．
