题目内容
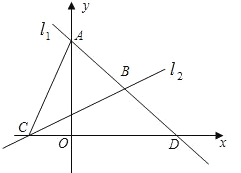
【题目】如图,抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)点P为抛物线上的一个动点,求使S△APC:S△ACD=5:4的点P的坐标.

【答案】(1)y=x2﹣2x﹣3.(2)满足条件的点的坐标为(4,5)或(﹣2,5).
【解析】
(1)先根据直线y=x-3求出A、B两点的坐标,然后将它们代入抛物线中即可求出待定系数的值.
(2)根据(1)中抛物线的解析式可求出C,D两点的坐标,由于△APC和△ACD同底,因此面积比等于高的比,即P点纵坐标的绝对值:D点纵坐标的绝对值=5:4.据此可求出P点的纵坐标,然后将其代入抛物线的解析式中,即可求出P点的坐标.
(1)直线y=x-3与坐标轴的交点A(3,0),B(0,-3).
则![]() ,
,
解得![]() ,
,
∴此抛物线的解析式y=x2-2x-3.
(2)抛物线的顶点D(1,-4),与x轴的另一个交点C(-1,0).
设P(a,a2-2a-3),则(![]() ×4×|a2-2a-3|):(
×4×|a2-2a-3|):(![]() ×4×4)=5:4.
×4×4)=5:4.
化简得|a2-2a-3|=5.
当a2-2a-3=5,得a=4或a=-2.
∴P(4,5)或P(-2,5),
当a2-2a-3<0时,即a2-2a+2=0,此方程无解.
综上所述,满足条件的点的坐标为(4,5)或(-2,5).

练习册系列答案
相关题目