题目内容
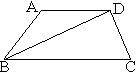
已知:如图,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4![]() ,求梯形的面积.
,求梯形的面积.
答案:
解析:
解析:
|
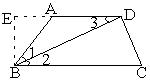
方法一:如图,
过点B作BE⊥DA交DA的延长线于E. ∵∠BAD= ∵BD平分∠ABC,∴∠1=∠2. ∵AD∥BC,∴∠3=∠2. ∴∠1=∠3= ∴在Rt△BDE中,∵BD=4 ∴BE= 在Rt△BEA中,AE=BE·cot ∴AD=ED-AE=6-2=4. ∴S梯形= 方法二:如图,
过点A作AE⊥BD于E,过点D作DF⊥BC于F. ∵BD平分∠ABC,∴∠1=∠2. ∵AD∥BC, ∴∠3=∠2.∴∠l=∠3. ∴AB=AD. ∵∠BAD= ∴∠2=∠3=∠1= ∵BD=4 ∴ED= 在Rt△AED中,AD= 在Rt△BFD中,DF= S梯形= |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目

 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )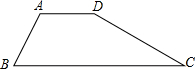 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=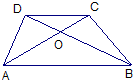 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.