题目内容
如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
(1)点D的坐标为D(2,6);(2)过O、D、B三点的抛物线的函数关系式为: .
.
解析试题分析:(1)过点D作DE⊥OA于E,可得到:△ADE∽△BAO,根据相似三角形的对应边成比例可求得点D坐标;
(2)根据△ADE∽△BAO,且AE=2,ED=2,可以得到:点B的坐标为B(0,4).设出函数解析式,将O、D、B三点坐标代入即可求出解析式.
试题解析:(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED= ,
,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(0,4)
设:过O、D、B三点的抛物线的函数关系式为:
将A(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为: .
.
考点:①三角形相似,②函数解析式.

练习册系列答案
相关题目
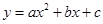 经过点A、B和D(4,
经过点A、B和D(4, ).
).
 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.

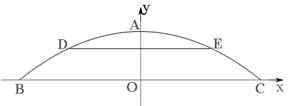


 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
 的两个根.
的两个根.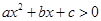 的解集.
的解集. 随
随 的增大而减小的自变量
的增大而减小的自变量 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围.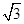 )为圆心,以2为半径的圆与
)为圆心,以2为半径的圆与 轴交于A、B两点.
轴交于A、B两点.
 的图象经过点A、B,试确定此二次函数的解析式.
的图象经过点A、B,试确定此二次函数的解析式.