题目内容
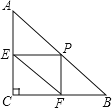
【题目】如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，P为AB边上（不与A、B重合的一动点，过点P分别作PE⊥AC于点E，PF⊥BC于点F，则线段EF的最小值是（ ）
A. 2B. 3C. 
D. 
【答案】C
【解析】
连接CP，利用勾股定理列式求出AB，判断出四边形CFPE是矩形，根据矩形的对角线相等可得EF=CP，再根据垂线段最短可得CP⊥AB时，线段EF的值最小，然后根据三角形的面积公式列出方程求解即可．
如图，连接CP．
∵∠C=90°，AC=3，BC=4，
∴AB=
=5，
∵PE⊥AC，PF⊥BC，∠C=90°，
∴四边形CFPE是矩形，
∴EF=CP，
由垂线段最短可得CP⊥AB时，线段EF的值最小，
此时，S△ABC=
BCAC=ABCP，
即×4×3=×5CP，
解得CP=2.4．
故选C．
练习册系列答案
相关题目
【题目】我们规定：有理数
用数轴上点
表示，叫做点在数轴上的坐标；有理数
用数轴上点
表示，叫做点在数轴上的坐标.
表示数轴上的两点，之间的距离.
（1）借助数轴，完成下表：
|
|
|
|
3 | 2 | 1 | 1 |
1 | 5 | ______ | ______ |
2 | －3 | ______ | ______ |
－4 | 1 | ______ | ______ |
－5 | －2 | ______ | ______ |
－3 | －6 | ______ | ______ |
（2）观察（1）中的表格内容，猜想
______；（用含，的式子表示，不用说理）
（3）已知点在数轴上的坐标是－2，且
，利用（2）中的结论求点在数轴上的坐标.
