题目内容
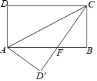
【题目】如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处.
(1)求证:△AFD′≌△CFB;
(2)求线段BF的长度;
(3)试求出重叠部分△AFC的面积.
【答案】(1)见解析;(2)BF=3;(3)10.
【解析】
(1)由翻折的性质可得AD’=CB,再由对顶角可得∠AFD’=∠CFB,再∠D’=∠B=90°,则可证两三角形全等;
(2)设BF为x,则由三角形全等可得CF=AF=8-x,题干已知BC=4,故利用勾股定理BC2+FB2=CF2可求解;
(3)求解出AF长度,以AF为底,BC长度为高,利用三角形面积公式即可求解.
解:(1)由折叠可得,∠D'=∠D=∠B=90°,AD'=AD=BC,
在△AD'F和△CBF中,
∵∠AFD’=∠CFB,∠D’=∠B=90°,AD’=CB,
∴△AFD≌△CFB(AAS);
(2)由折叠可得,∠ACF=∠ACD,
∵CD∥AB,
∴∠CAF=∠ACD,
∴∠ACF=∠CAF,
∴AF=CF,
设BF=x,则AF=CF=8﹣x,
∵∠B=90°,
∴在Rt△BCF中,BF2+CB2=CF2,
即42+x2=(8﹣x)2,
解得x=3,
∴BF=3;
(3)∵AF=8﹣3=5,BC=4,CB⊥AF,
∴S△ACF=![]() AF×BC=
AF×BC=![]() ×5×4=10.
×5×4=10.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目