题目内容
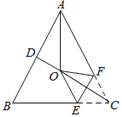
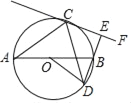
【题目】已知:如图,AB为⊙O的直径,C,D是⊙O直径AB异侧的两点,AC=DC,过点C与⊙O相切的直线CF交弦DB的延长线于点E.
(1)试判断直线DE与CF的位置关系,并说明理由;
(2)若∠A=30°,AB=4,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先证明△OAC≌△ODC,得出∠1=∠2,则∠2=∠4,故OC∥DE,即可证得DE⊥CF;
(2)根据OA=OC得到∠2=∠3=30°,故∠COD=120°,再根据弧长公式计算即可.
解:(1)DE⊥CF.
理由如下:
∵CF为切线,
∴OC⊥CF,
∵CA=CD,OA=OD,OC=OC,
∴△OAC≌△ODC,
∴∠1=∠2,
而∠A=∠4,
∴∠2=∠4,
∴OC∥DE,
∴DE⊥CF;
(2)∵OA=OC,
∴∠1=∠A=30°,
∴∠2=∠3=30°,
∴∠COD=120°,
∴![]() 的长=
的长=![]() =
=![]() π.
π.

练习册系列答案
相关题目