题目内容
已知一次函数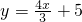 的图象与x轴交于A点,
的图象与x轴交于A点,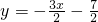 的图象与y轴交于B点,这两个一次函数的图象相交于P点,则△ABP的面积是________.
的图象与y轴交于B点,这两个一次函数的图象相交于P点,则△ABP的面积是________.

分析:先根据直线解析式求出点A、B的坐标,联立两函数解析式求解得到点P的坐标,设直线y=-
 x-
x- 与x轴的交点为C,求出点C的坐标,然后求粗AC的长度,再根据S△ABP=S△APC+S△ABC,列式计算即可得解.
与x轴的交点为C,求出点C的坐标,然后求粗AC的长度,再根据S△ABP=S△APC+S△ABC,列式计算即可得解.解答:
 解:令y=0,则
解:令y=0,则 +5=0,
+5=0,解得x=-
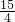 ,
,令x=0,则y=-
 ,
,所以,点A(-
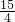 ,0),B(0,-
,0),B(0,- ),
),联立
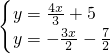 ,
,解得
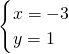 ,
,所以,点P(-3,1),
设直线y=-
 x-
x- 与x轴的交点为C,
与x轴的交点为C,令y=0,则-
 x-
x- =0,
=0,解得x=-
 ,
,所以,点C(-
 ,0),
,0),AC=-
 -(-
-(-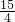 )=-
)=- +
+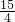 =
=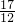 ,
,S△ABP=S△APC+S△ABC,
=
 ×
×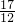 ×1+
×1+ ×
×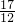 ×
× ,
,=
 +
+ ,
,=
 .
.故答案为:
 .
.点评:本题考查了两直线相交的问题,主要涉及直线与坐标轴的交点的求解,联立两直线解析式求交点坐标以及求三角形的面积的方法,难点较大,把△ABP的面积分成两个三角形的面积求解比较关键.

练习册系列答案
相关题目
已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( )
| A、y=-x-2 | B、y=-x-6 | C、y=-x+10 | D、y=-x-1 |
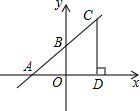 在第一象限,CD⊥x轴于D,若OA=OB=OD=1.
在第一象限,CD⊥x轴于D,若OA=OB=OD=1.