Question

(本题12分) 在正方形网格中，A、B为格点，以点为圆心，为半径作圆交网格线于点(如图(1))，过点作圆的切线交网格线于点，以点为圆心，为半径作圆交网格线于点(如图(2))．

 

 

 

 

 

 

问题：

1.(1) 求的度数；

2.(2) 求证：；

3.(3) 可以看作是由经过怎样的变换得到的？并判断的形状(不用说明理由)．

4.(4) 如图(3)，已知直线，且a∥b，b∥c，在图中用直尺、三角板、圆规画等边三角形，使三个顶点，分别在直线上．要求写出简要的画图过程，不需要说明理由．

 

 

 

 

 

 

 

Answer 1

【答案】

 

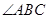1.（1）=60°

2.略

3.（3）是由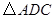绕点A顺时针旋转60°得到的. 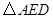是等边三角形.

 

4.（4）①在直线a上任取一点，记为点A′，作A′M′⊥b，垂足为点M′；②作线段A′M′的垂直平分线，此直线记为直线d；③以点A′为圆心，A′M′长为半径画圆，与直线d交于点N′；④过点N′作N′C′⊥A′N′交直线c于点C′；⑤以点A′为圆心，A ′C′ 长为半径画圆，此圆交直线b于点B′；

连接A′B′、B′C′，则△A′B′C′为所求等边三角形

【解析】略