题目内容
(本题满分12分)在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t. 
【小题1】⑴ 求tan∠FOB的 值;
值;
【小题2】⑵用含t的代数式表示△OAB的面积S;
【小题3】⑶是否存在点C,使以B,E,F为顶点的三角形与△OFE相似,若存在,请求出所有满足要求的B点的坐标;若不存在,请说明理由.
【小题1】解:(1)∵A(2,2) ∴∠AOB=45° ∴CD=OD=DE=EF= ∴
∴
【小题2】(2)由△ACF~△AOB得 ∴
∴ ∴
∴
【小题3】(3)要使△BEF与△OFE相似,∵∠FEO=∠FEB=90°,∴只要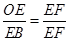 或
或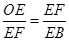 ,即:
,即: 或
或
① 当 时,
时,  ,∴
,∴ ∴
∴ (舍去)或
(舍去)或 ∴B(6,0)
∴B(6,0)
② 当 时,
时,
(ⅰ)当B在E的左侧时, , ∴
, ∴ ∴
∴ (舍去)或
(舍去)或 ∴B(1,0)
∴B(1,0)
(ⅱ)当B在E的右侧时, , ∴
, ∴ ∴
∴ (舍去)或
(舍去)或 ∴B(3,0)
∴B(3,0)
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由。
(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由。 经过点(0,10)
经过点(0,10)
 中,已知二次函数
中,已知二次函数 的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3). (3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
(3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由