题目内容
(本题12分)如图,在平面直角坐标系中,等腰梯形OABC,CB//OA,且点A在x轴正半轴上.已知C(2,4),BC= 4.(1)求过O、C、B三点的抛物线解析式,并写出顶点坐标和对称轴;
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合),使得P点到两坐标轴的
距离相等.如果存在,求出P点坐标;如果不存在,请说明理由.

解:(1) ( 6分)∵C(2,4), BC="4" 且 BC//OA ∴ B(6,4) 1分
设抛物线为
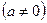
将O(0,0),C(2,4),B(6,4)代入得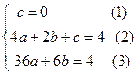 解得
解得 3分
3分
∴ 1分
1分
∴顶点 对称轴:直线
对称轴:直线 2分
2分
(2) (6分)据题意,设 或
或
 1分
1分
将 代入抛物线得
代入抛物线得 解得
解得 (舍) 2分
(舍) 2分
将 代入抛物线得
代入抛物线得 解得
解得 (舍) 2分
(舍) 2分
∴符合条件的点 和
和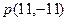 1分解析:
1分解析:
略
设抛物线为

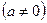
将O(0,0),C(2,4),B(6,4)代入得
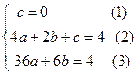 解得
解得 3分
3分∴
 1分
1分∴顶点
 对称轴:直线
对称轴:直线 2分
2分(2) (6分)据题意,设
 或
或
 1分
1分将
 代入抛物线得
代入抛物线得 解得
解得 (舍) 2分
(舍) 2分将
 代入抛物线得
代入抛物线得 解得
解得 (舍) 2分
(舍) 2分∴符合条件的点
 和
和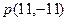 1分解析:
1分解析:略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=