题目内容
 21、已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
21、已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.(1)求证:CP=AE;
(2)问PB与BE有怎样的位置关系,请说明理由.
分析:(1)利用正方形的特殊性质,证明△CBP≌△ABE得出CP=AE;
(2)∠CBP=∠ABE是证明PB⊥BE的关键.
(2)∠CBP=∠ABE是证明PB⊥BE的关键.
解答:证明:(1)∵四边形ABCD是正方形,
∴BC=AB;
∵∠CBP=∠ABEBP=BE,
∴△CBP≌△ABE,
∴CP=AE.
(2)PB与BE的关系是PB⊥BE.
∵∠CBP=∠ABE,
∴∠PBE=∠ABE+∠ABP=∠CBP+∠ABP=90°,
∴PB⊥BE.
∴BC=AB;
∵∠CBP=∠ABEBP=BE,
∴△CBP≌△ABE,
∴CP=AE.
(2)PB与BE的关系是PB⊥BE.
∵∠CBP=∠ABE,
∴∠PBE=∠ABE+∠ABP=∠CBP+∠ABP=90°,
∴PB⊥BE.
点评:解答本题要充分利用正方形的特殊性质,同时考查了全等三角形的判定和性质.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 4,6),且AB=
4,6),且AB=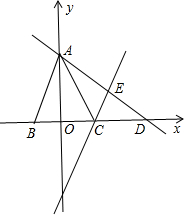 将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D.
将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D. 已知:如图,一次函数y=
已知:如图,一次函数y= 已知:如图所示,直线l的解析式为
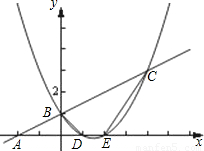
已知:如图所示,直线l的解析式为 x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)