题目内容
若O为△ABC的外心，I为三角形的内心，且∠BIC=110°，则∠BOC=（ ）
| A．70° | B．80° | C．90° | D．100° |
B
∵I是△ABC的内心，
∴∠IBC=
∠ABC，∠ICB=∠ACB．
∵∠ABC+∠ACB=180°-∠A，
∠IBC+∠ICB+∠BIC=180°，
∴∠BIC=180°-（∠IBC+∠ICB）=180°-（∠ABC+∠ACB）
=180°-（180°-∠A）=90°+∠A．
∴∠BIC=90°+∠A=90°+×∠BOC=90°+
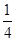∠BOC
∵∠BIC=110°
∴∠BOC=80°
故选B
∴∠IBC=
∠ABC，∠ICB=∠ACB．∵∠ABC+∠ACB=180°-∠A，
∠IBC+∠ICB+∠BIC=180°，
∴∠BIC=180°-（∠IBC+∠ICB）=180°-（
∠ABC+∠ACB）=180°-
（180°-∠A）=90°+∠A．∴∠BIC=90°+
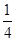∠A=90°+×∠BOC=90°+∠BOC∵∠BIC=110°
∴∠BOC=80°
故选B
练习册系列答案
天天向上一本好卷系列答案
相关题目
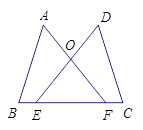
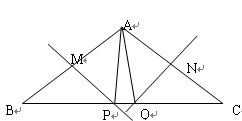
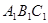与△ABC关于直线
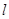对称，将△
，由此得到下列判断：①AB∥
；②∠A=∠
；③AB=
