题目内容
【题目】如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
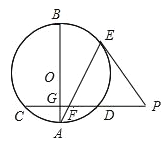
(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
【答案】(1)PE=PF;(2)圆O的直径为![]() .
.
【解析】试题分析:(1)如图1,连接OE,根据切线的性质得出∠PEO=90°,求出∠PEF=∠PFE,根据等腰三角形的判定得出即可;
(2)如图2,连接BE,根据相似三角形的判定得出△AGF∽△AEB,得出比例式,代入求出即可.
试题解析:(1)证明:如图1,连接OE,
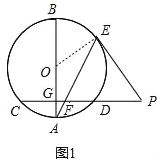
∵EP是⊙O的切线,
∴∠PEO=90°,
∴∠OEA+∠PEF=90°,
∵AB⊥CD,
∴∠AGF=90°,
∴∠A+∠AFG=90°,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠PEF=∠AFG,
∵∠EFP=∠AFG,
∴∠PEF=∠PFE,
∴PE=PF;
(2)解:如图2,连接BE,
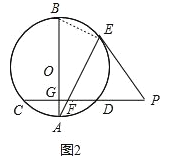
∵AB为直径,
∴∠AEB=90°,
∵∠AGF=90°,
∴∠AGF=∠AEB,
∵∠A=∠A,
∴△AGF∽△AEB,
∴![]() ,
,
∵AG=4,AF=5,EF=25,
∴![]() ,
,
∴AB=![]() ,
,
即圆O的直径为![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目