Question

【题目】如图，在Rt△ABC中，∠ACB=90°，BD是∠ABC的平分线，点O在AB上，⊙O经过B，D两点，交BC于点E．

（1）求证：AC是⊙O的切线；

（2）若AB=6，sin∠BAC=，求BE的长．

Answer 1

【答案】（1）证明见解析；（2）3.2.

【解析】试题分析：（1）连接DO，由等腰三角形的性质和角平分线的定义得出∠1=∠3，证出DO∥BC，由平行线的性质得出∠ADO=90°，即可得出结论；

（2）设⊙O的半径为R，由三角函数求出BC，由平行线得出△AOD∽△ABC，得出对应边成比例，求出半径OD，过O作OF⊥BC于F，则BE=2BF，如图所示：则OF∥AC，由平行线的性质得出∠BOF=∠BAC，由三角函数求出BF，即可得出结果．

试题解析：（1）连接DO，如图1所示

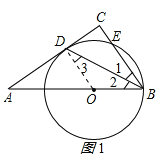
∵BD是∠ABC的平分线，

∴∠1=∠2，

∵OB=OD，

∴∠2=∠3，

∴∠1=∠3，

∴DO∥BC，

∵∠C=90°，

∴∠ADO=90°，

即AC⊥OD，

∴AC是⊙O的切线．

（2）设⊙O的半径为R，

在Rt△ABC中，∠ACB=90°，sin∠BAC=，

∴BC=×6=4，

由（1）知，OD∥BC，

∴△AOD∽△ABC，

∴，

∴，

解得：R=2.4，

过O作OF⊥BC于F，如图所示：

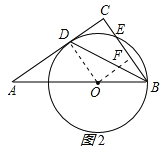
则BE=2BF，OF∥AC，

∴∠BOF=∠BAC，

∴sin∠BOF=，

∴BF=×2.4=1.6，

∴BE=2BF=3.2．