题目内容
【题目】如图1是“东方之星”救援打捞现场图,小红据此构造出一个如图2所示的数学模型,已知:A、B、D三点在同一水平线上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.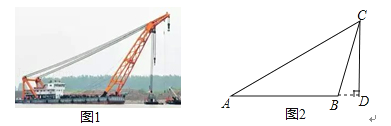
(1)求点B到AC的距离.
(2)求线段CD的长度.
【答案】
(1)
解:过点B作BE⊥AC于点E,
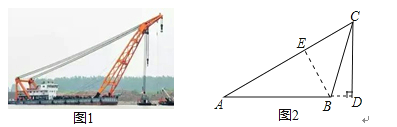
在Rt△AEB中,AB=60m,sinA=![]() ,BE=ABsinA=60×
,BE=ABsinA=60×![]() =30,cosA=
=30,cosA=![]() ,
,
∴AE=60×![]() =30
=30![]() m,
m,
在Rt△CEB中,∠ACB=∠CBD﹣∠A=75°﹣30°=45°,
∴BE=CE=30m
∴点B到AC的距离为30m.
(2)
解:
过点B作BE⊥AC于点E,

在Rt△AEB中,AB=60m,sinA=![]() ,BE=ABsinA=60×
,BE=ABsinA=60×![]() =30,cosA=
=30,cosA=![]() ,
,
∴AE=60×![]() =30
=30![]() m,
m,
在Rt△CEB中,∠ACB=∠CBD﹣∠A=75°﹣30°=45°,
∴BE=CE=30m,
∴AC=AE+CE=(30+30![]() )m,
)m,
在Rt△ADC中,sinA=![]() ,
,
则CD=(30+30![]() )×
)×![]() =(15+15
=(15+15![]() )m.
)m.
【解析】过点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长,由AE+CE求出AC的长,即可求出CD的长.
此题考查了构造直角三角形利用三角函数求线段长的知识点.

练习册系列答案
相关题目
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.