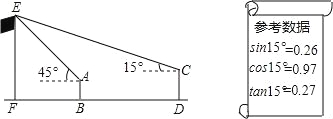
题目内容
【题目】如图,已知AB是⊙O的直径,弦AC平分∠DAB,过点C作直线CD,使得CD⊥AD于D.
(1)求证:直线CD与⊙O相切;
(2)若AD=3,AC=![]() ,求直径AB的长.
,求直径AB的长.
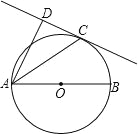
【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA,接着利用平行线的判定即可得到OC∥AD,然后就得到OC⊥CD,由此即可证明直线CD与⊙O相切于C点;
(2)连接BC,根据圆周角定理的推理得到∠ACB=90°,又∠DAC=∠OAC,由此可以得到△ADC∽△ACB,然后利用相似三角形的性质即可解决问题.
试题解析:(1)连接OC,∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠DAB
∴∠DAC=∠OAC,∴∠DAC=∠OCA,∴OC∥AD,∵AD⊥CD,,∴OC⊥CD.
又∵OC是⊙O的半径,∴直线CD与⊙O相切于点C
(2)连接BC,则∠ACB=90°.∵∠DAC=∠OAC,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,∴![]() ,∴AB=
,∴AB=![]() =4.
=4.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目