题目内容
已知A(x1,y1),B(x2,y2)在二次函数y=x2-6x+4的图象上,若x1<x2<3,则y1 y2(填“>”、“=”或“<”).
考点:二次函数图象上点的坐标特征
专题:
分析:先求出二次函数的对称轴为直线x=3,再根据二次函数的增减性解答.
解答:解:二次函数的对称轴为直线x=-
=3,
∵a=1>0,
∴当x<3时,y随x的增大而减小,
∵x1<x2<3,
∴y1>y2.
故答案为:>.
| -6 |
| 2×1 |
∵a=1>0,
∴当x<3时,y随x的增大而减小,
∵x1<x2<3,
∴y1>y2.
故答案为:>.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性,熟记性质并求出二次函数的对称轴是解题的关键.

练习册系列答案
相关题目
|2014|的值是( )
| A、-2014 | ||
| B、2014 | ||
C、
| ||
D、-
|
若正多边形的一个外角等于45°,那么这个正多边形的内角和等于( )
| A、1 080° |
| B、720° |
| C、540° |
| D、360° |
不等式x+3≥0有( )个负整数解.
| A、1 | B、2 | C、3 | D、4 |
 如图,BO、CO分别为∠ABC、∠ACB的外角平分线,且∠BOC=60°,则∠A=
如图,BO、CO分别为∠ABC、∠ACB的外角平分线,且∠BOC=60°,则∠A=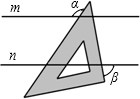 小明同学把一个含有45°角的直角三角板放在如图的两条平行线m,n上,测得∠α=120°,则∠β的度数是
小明同学把一个含有45°角的直角三角板放在如图的两条平行线m,n上,测得∠α=120°,则∠β的度数是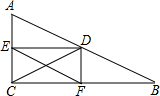 在Rt△ABC中,∠ACB=90°,D是AB的中点,DE平分∠ADC,DF平分∠BDC,那么EF=DC吗?试说明理由.
在Rt△ABC中,∠ACB=90°,D是AB的中点,DE平分∠ADC,DF平分∠BDC,那么EF=DC吗?试说明理由.