Question

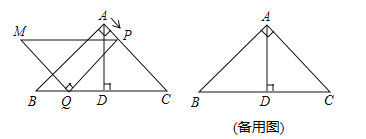
【题目】如图，点A，C都在直线l上，AE⊥AB且AE=AB，BC⊥CD且BC=CD，三点E，B，D到直线l的距离分别是6，3，4，计算图中由线段AB，BC，CD，DE，EA所围成的图形的面积是（　　）

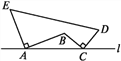
A. 50 B. 62 C. 65 D. 68

Answer 1

【答案】A

【解析】首先根据题意，过点E，B，D分别作EF⊥l，BG⊥l，DH⊥l，点F，G，H分别为垂足由AE⊥AB，EF⊥FH，BG⊥AG，可以得到∠EAF=∠ABG，而AE=AB，∠EFA=∠AGB，由此可以证明△EFA≌△ABG，所以AF=BG，AG=EF；同理证得△BGC≌△DHC，GC=DH，故CH=BG，FH=FA+AG+GC+CH=3+6+4+3=16，然后利用面积的割补法和面积公式，即可求出图形的面积．

解：如图，过点E，B，D分别作EF⊥l，BG⊥l，DH⊥l，点F，G，H分别为垂足，

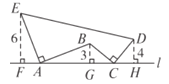
∵AE⊥AB且AE=AB，EF⊥FH，BG⊥FH，

∴∠EAB=∠EFA=∠BGA=90°，

∴∠EAF+∠BAG=90°，∠ABG+∠BAG=90°，

∴∠EAF=∠ABG，

∵AE=AB，∠EFA=∠AGB，∠EAF=∠ABG，

∴△EFA≌△ABG，

∴AF=BG，AG=EF．

同理证得△BGC≌△DHC得GC=DH，CH=BG．

故FH=FA+AG+GC+CH=3+6+4+3=16．

故S=×(6+4)×16-3×4-6×3=50.

故选A.