题目内容
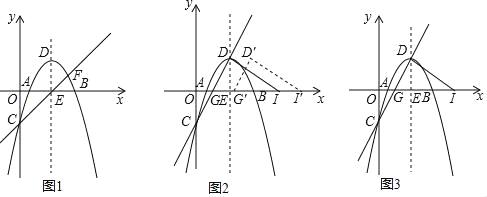
【题目】如图,一条直线与反比例函数![]() 的图象交于A(1,4),B(4,n)两点,与x轴交于点D,AC⊥x轴,垂足为C.
的图象交于A(1,4),B(4,n)两点,与x轴交于点D,AC⊥x轴,垂足为C.

(1)求反比例函数的解析式及D点的坐标;
(2)点P是线段AD的中点,点E,F分别从C,D两点同时出发,以每秒1个单位的速度沿CA,DC运动,到点A,C时停止运动,设运动的时间为t(s).
①求证:PE=PF.②若△PEF的面积为S,求S的最小值.
【答案】(1)![]() ,D(5,0);(2)①证明见试题解析;②2.
,D(5,0);(2)①证明见试题解析;②2.
【解析】
(1)把点A的坐标代入![]() 求出k的值,即可得出反比例函数的解析式;求出点B的坐标,再求出直线AB的解析式,即可求出D点的坐标;
求出k的值,即可得出反比例函数的解析式;求出点B的坐标,再求出直线AB的解析式,即可求出D点的坐标;
(2)①由△ACD为等腰直角三角形,得出∠ADC=45°,得出CP=PD,CP⊥AD,∠ADC=∠ACP,即可得出△ECP≌△FDP,从而有PE=PF;
②由△ECP≌△FDP,得出∠EPC=∠FPD,得出∠EPF=∠CPD=90°,得到△EPF为等腰直角三角形,从而有△PEF的面积S=![]()
![]() ,当PE⊥AC时,PE最小,求出PE的最小值,即可得出S的最小值.
,当PE⊥AC时,PE最小,求出PE的最小值,即可得出S的最小值.
(1)把点A(1,4)代入![]() 得:k=4,∴反比例函数的解析式为:
得:k=4,∴反比例函数的解析式为:![]() ;把点B(4,n)代入得:n=1,∴B(4,1),设直线AB的解析式为y=kx+b,把A(1,4),B(4,1)代入y=kx+b得:
;把点B(4,n)代入得:n=1,∴B(4,1),设直线AB的解析式为y=kx+b,把A(1,4),B(4,1)代入y=kx+b得:![]() ,解得:k=﹣1,b=5,∴直线AB的解析式为:y=﹣x+5,当y=0时,x=5,∴D点坐标为:(5,0);
,解得:k=﹣1,b=5,∴直线AB的解析式为:y=﹣x+5,当y=0时,x=5,∴D点坐标为:(5,0);
(2)①∵A(1,4),C(1,0 ),D(5,0),AC⊥x轴于C,∴AC=CD=4,∴△ACD为等腰直角三角形,∴∠ADC=45°,∵P为AD中点,∴∠ACP=∠DCP=45°,CP=PD,CP⊥AD,∴∠ADC=∠ACP,∵点E,F分别从C,D两点同时出发,以每秒1个单位的速度沿CA,DC运动,∴EC=DF,在△ECP和△FDP中,∵CP=PD,∠ECP=∠PDF,EC=DF,∴△ECP≌△FDP(SAS),∴PE=PF;
②∵△ECP≌△FDP,∴∠EPC=∠FPD,∴∠EPF=∠CPD=90°,∴△PEF为等腰直角三角形,∴△PEF的面积S=![]()
![]() ,∴△PEF的面积最小时,EP最小,∵当PE⊥AC时,PE最小,此时EP最小值=
,∴△PEF的面积最小时,EP最小,∵当PE⊥AC时,PE最小,此时EP最小值=![]() CD=2,∴△PEF的面积S的最小值=
CD=2,∴△PEF的面积S的最小值=![]() =2.
=2.

 名校课堂系列答案
名校课堂系列答案【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为400人,如表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 1600本 | B |
名人传记 | 1280本 | 0.32 |
漫画丛书 | A本 | 0.24 |
其它 | 160本 | 0.04 |
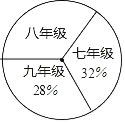
(1)求该校八年级的人数占全校总人数的百分率为 ;
(2)表中A= ,B= ;
(3)该校学生平均每人读多少本课外书?