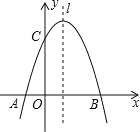
题目内容
【题目】在等腰直角三角形ABC左侧作直线AP,点B关于直线AP的对称点为D,连结BD、CD,其中CD交直线AP于点E.
(1)依题意补全图1;
(2)若∠PAB=28°,求∠ACD的度数;
(3)如图2,若45°<∠PAB <90°,用等式表示线段AB,CE,DE之间的数量关系,并证明.
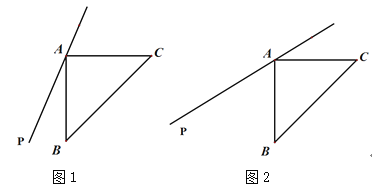
【答案】(1)图形见解析(2)17°(3)CE+DE=2AB
【解析】试题分析:(1)根据题意直接画出图形得出即可;
(2)利用对称的性质以及等角对等边进而得出答案;
(3)由轴对称的性质可得:BE=DE,AC=AB=AD,∠ABF=∠ACE=∠ADF,得到∠BEC=∠BAC=90°,进而利用勾股定理得出答案.
试题解析:解:(1)如图1所示:
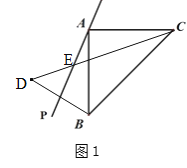
(2)如图2,连接AD,则∠PAB=∠PAD=28°,AC=AB=AD,∵∠BAC=90°,∠PAB=∠PAD=28°,∴∠CAD=146°,∴∠ACD=(180°-146°)÷2=17°;
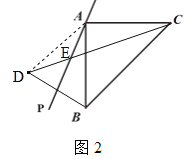
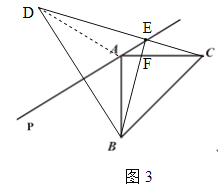
(3)如图3,连接AD 、BE,由轴对称的性质可得:BE=DE,AC=AB=AD,∠ABF=∠ACE=∠ADF,∵∠AFB=∠CFE,∴∠BEC=∠BAC=90°,∴BF2+E2=BC2,∴EC2+DE2=2AB2.

练习册系列答案
相关题目
【题目】小康水平的一个指标是年人均收入1000美元.2008年对某地进行随机抽样调查,得出10户年人均收入,若以人均1000美元以上为达到小康指标,超过1000美元的美元数用正数表示,不足1000美元的美元数用负数表示,此10户的年人均收入如下(单位:美元):
+500 | -300 | +200 | 0 | +1000 | -100 | +400 | -200 | +100 | +100 |
(1)请你算一下这10户有百分之多少达到了小康指标?
(2)10户年平均收入为多少美元?