题目内容
【题目】(本小题满分9分)
已知二次函数y=x2–4x+3.
(1)求出函数的顶点坐标,对称轴,以及与x轴的交点,并据此作出函数的图象;
(2)当1<x<5时,求y的取值范围.
【答案】见解析
【解析】(1)y=x2–4x+3=(x–2)2–1,(1分)
则函数顶点坐标是(2,–1),(2分)
函数的对称轴是x=2,(3分)
方程x2–4x+3=0的根是x1=1,x2=3.
则函数与x轴的交点是(1,0)和(3,0).(4分)
则抛物线y=x2–4x+3的图象如下图所示:
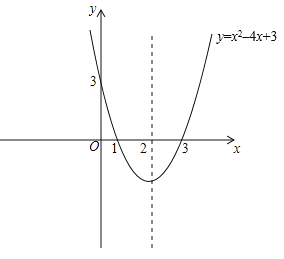 ;(6分)
;(6分)
(2)由(1)可知,函数顶点坐标是(2,–1),
即当1<x<5时,函数有最小值–1,(8分)
当x=5时,y=25–20+3=8,
则当1<x<5时,y的范围是–1≤y<8.(9分)

练习册系列答案
相关题目

