题目内容
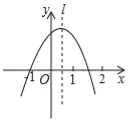
【题目】(本小题满分11分)如图,已知抛物线y=x2+bx+c经过A(–1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

【答案】见解析
【解析】(1)把A(–1,0)、B(3,0)分别代入y=x2+bx+c中,
得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为y=x2–2x–3.(2分)
∵y=x2–2x–3=(x–1)2–4,
∴抛物线的顶点坐标为(1,–4).(3分)
(2)由图可得当0<x<3时,–4≤y<0.(5分)
(3)∵A(–1,0)、B(3,0),
∴AB=4.
设P(x,y),则S△PAB=![]() AB|y|=2|y|=10,
AB|y|=2|y|=10,
∴|y|=5,
∴y=±5.(7分)
①当y=5时,x2–2x–3=5,解得:x1=–2,x2=4,
此时P点坐标为(–2,5)或(4,5);(9分)
②当y=–5时,x2–2x–3=–5,方程无解;
综上所述,P点坐标为(–2,5)或(4,5).(11分)

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目