题目内容
【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y= ![]() .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
【答案】
(1)
解:当40≤x<60时,W=(x﹣30)(﹣2x+140)=﹣2x2+200x﹣4200,
当60≤x≤70时,W=(x﹣30)(﹣x+80)=﹣x2+110x﹣2400
(2)
解:当40≤x<60时,W=﹣2x2+200x﹣4200=﹣2(x﹣50)2+800,
∴当x=50时,W取得最大值,最大值为800万元;
当60≤x≤70时,W=﹣x2+110x﹣2400=﹣(x﹣55)2+625,
∴当x>55时,W随x的增大而减小,
∴当x=60时,W取得最大值,最大值为:﹣(60﹣55)2+625=600,
∵800>600,
∴当x=50时,W取得最大值800,
答:该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元
(3)
解:当40≤x<60时,由W≥750得:﹣2(x﹣50)2+800≥750,
解得:45≤x≤55,
当60≤x≤70时,W的最大值为600<750,
∴要使企业销售该产品的年利润不少于750万元,该产品的售价x(元/件)的取值范围为45≤x≤55
【解析】(1)根据:年利润=(售价﹣成本)×年销售量,结合x的取值范围可列函数关系式;(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案;(3)根据题意知W≥750,可列关于x的不等式,求解可得x的范围.本题主要考查二次函数的实际应用,梳理题目中的数量关系,得出相等关系后分情况列出函数解析式,熟练运用二次函数性质求最值是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
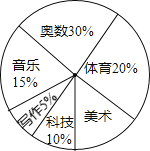
学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
人数 | 72 | 36 | 54 | 18 |
(1)七年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;
(4)众数是 .